The simplest kind of wave is the longitudinal wave. Sound waves in air are longitudinal waves, meaning the direction of particle vibration is the same as the direction of wave propagation.
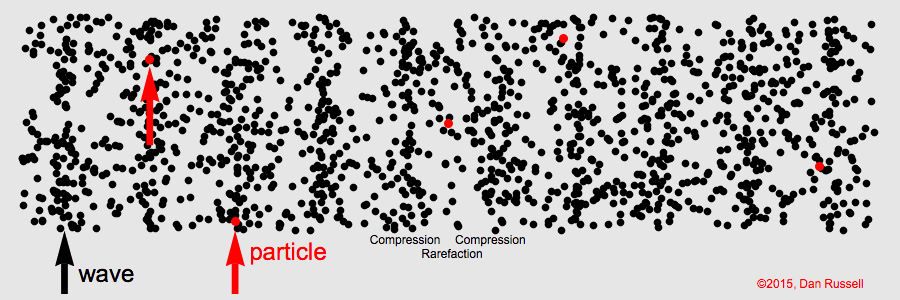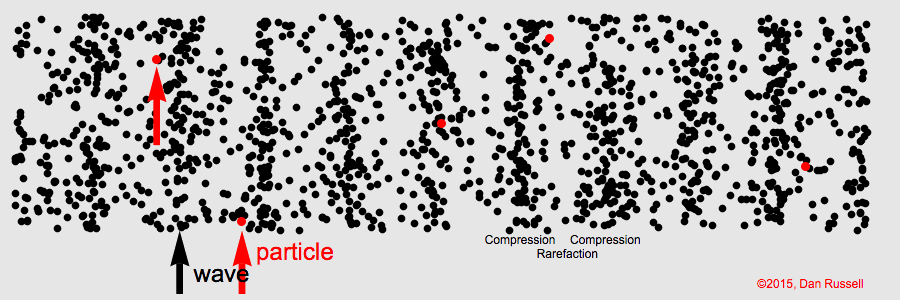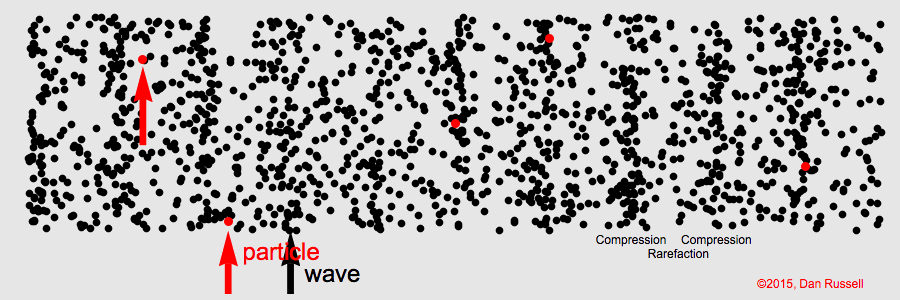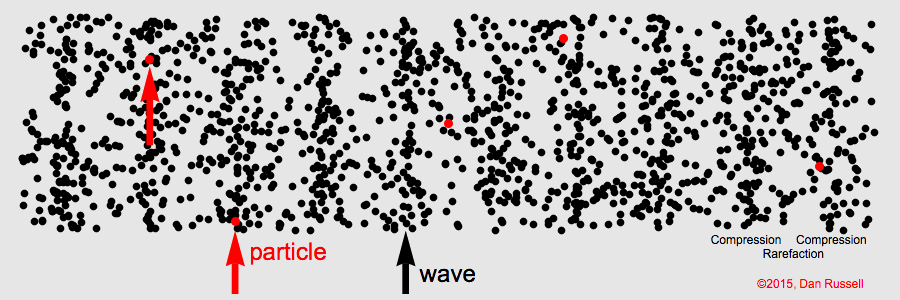
Plane waves are often used to model sound waves in ducts or at distances far from a source where the wavefront curvature can be neglected. Langevin transducers are an example application of longitudinal waves, although they are not the only type of waves in operation.
The speed of sound, C, is the rate at which a sound wave propagates through a medium. It depends on the properties of the medium, such as its temperature, density, and elasticity. In dry air at 20°C, the speed of sound is approximately 343 m/s.
An important equation to calculate the speed of sound in a material uses the material's modulus of elasticity, M, N/m2, and density, D, kg/m3. The modulus of elasticity should be chosen most relevant to the type of wave. A useful table can be found in Wikipedia. Usually the Young's Modulus is given for materials, and using the Poisson's ratio, this can be converted to the correct and relevnt modulus.
\[ c = \sqrt{M/D} \]
It can be observed from the illustration below of the different types of moduli, how each type could be related to a particular type of wave. For example, the Bulk modulus sees pressure from all directions which is what happends in a Body wave. While on the other hand, if we are concerned with longitudinal waves, we would need to look at a constrained modulus, M, which strictly looks at the change in stress and strain in one direction.

The most important aspects of a sound wave can be split into frequency and time domain characteristics. In the frequency domain, it is frequency and wavelength. In the time domain, it is the phase. The frequency, f, of a sound wave is the number of cycles of pressure variations per second. It is measured in Hertz (Hz), where 1 Hz represents one cycle per second. The wavelength, λ, of a sound wave is the distance between two consecutive points in the wave that are in the same phase. The relationship between speed of sound, frequency, and wavelength is given by:
\[ c = \lambda f \]
This equation shows that wavelength is inversely proportional to frequency. Higher-frequency sounds have shorter wavelengths, and lower-frequency sounds have longer wavelengths.
Usually a good starting point is to assume a plane wave when studying acoustics, for the sake of mathematical simplicity and usefulness in deriving the fundamentals. A plane wave going in one direction can be represented by the following equation:
$$ Ae^{i(\omega t -kx) } = \cos ({\omega t -kx}) + i (\sin {\omega t -kx}) $$
The easiest way to understand the above if you are from a non-mathematical background is to imagine a dot travelling around a circle, illustrated below. The plane wave described above has 2 of those "phasors," one is for time (wt) and another for space(kx). When a plane wave travels as illustrated above, there is a pressure change and particle velocity. Pressure and velocity define the impedance, intensity and power of a wave, which are qualities that are more related to energy rather than just pressure or velocity.

Generally in acoustics, the acoustic impedance, Z, is the ratio of sound pressure to particle velocity. It measures the relationship between pressure and velocity. A useful parameter used in acoustics is the specific acoustic impedance, z, is a type of impedance usually used to characterise the medium. For a plane travelling wave, the specific acoustic impedance is equal to the product of the density of the medium, \rho, and the speed of sound (c) in the medium. This quantity is also called the characteristic impedance of the medium. It can already be observed that denser materials with higher speeds of sounds have higher impedance. It will become clearer why this is important in the following section, when we assess how a wave might travel from medium to another.
\[ Z = p/u = \pm \rho_0 c \]
As a result of the equation above, we can see in a plane wave, there is no phase difference between velocity and pressure. This means the impedance is constant and the power is maximum e.g. power output = p*u. This is a simplification only but useful as starting point. See Bies and Hansen eq. 1.18.

Using the characteristics of the plane wave described above, now we can derive useful equations about reflection and transmission of a wave. The reflection coefficient (R) is a measure of how much of a sound wave is reflected back when it encounters a boundary between two media with different acoustic impedances. The transmission coefficient (T) is a measure of how much of the sound wave is transmitted through the boundary. Both coefficients depend on the specific acoustic impedances of the two media.
For reference, here is a table of some common media we might encounter in our calculation over the next section.
| No. | Materials | Density (kg/m³) | Sound speed (m/s) | Impedance (Rayl) |
|---|---|---|---|---|
| 1 | Air | 1.23 | 340 | 418 |
| 2 | Water | 1053 | 1490 | 1.56 x 10⁶ |
| 3 | Cork | 0.24 | 530 | 1.27 x 10⁵ |
| 4 | Aluminum | 2690 | 6420 | 1.73 x 10⁷ |
| 5 | Steel | 7860 | 5950 | 4.64 x 10⁷ |
| 6 | PDMS | 969 | 1119 | 1.08 x 10⁶ |
| 7 | PU | 1528 | 1040 | 1.59 x 10⁶ |
| 8 | Epoxy | 1180 | 2490 | 2.95 x 10⁶ |
| 9 | Hydrogel | 1000 | 1600 | 1.60 x 10⁶ |
| 10 | Ecoflex | 1070 | 989 | 1.06 x 10⁶ |
Let's take an example from the illustration. We have a transducer emitting waves from air which then encounter a body of water. We have the specific acoustic impedance Zair and Zwater or we can call them Z1 and Z2. Then the reflection and transmission coefficients can be calculated as follows.
$$ |R| = \frac{(|Z_1 - Z_2|)^2}{(|Z_1 + Z_2|)^2} $$
$$ T = \frac{2Z_2}{(Z_2 + Z_1)} $$
Use the values above and experiment using the equations given. Note T and R are both dimensionless e.g. can be expressed as percentages and have no units. In summary, we have 3 possibilities:
$$ Z_1 = Z_2 \rightarrow R = 0, T = 1 $$ This means no reflected wave, and transmitted wave = 1, so everything is transmitted.
$$ Z_2 > Z_1 \rightarrow R > 0, T > 1 $$ This means the reflected wave is in phase with the incident wave. This is reminiscent of the string reflection from a free end. The transmitted wave is in phase with the incident wave at the boundary. Transmitted wave amplitude depends on the difference between the two.
$$ Z_2 < Z_1 \rightarrow R < 0, T < 1 $$ The reflected wave is 180° out of phase with the incident wave. This is reminiscent of the string reflection from a rigid end. The transmitted wave is in phase with the incident wave at the boundary. Transmission dependent on magnitude of difference between the two.
$$ Z_2 / Z_1 = \infty, Z_2 >> Z_1 \rightarrow R = +1 , T = 2 $$ All energy reflected at boundary because the reflection coefficient is +1 and the amplitude of the reflected wave is the amplitude of the incident wave. Medium 2 is virtually incompressible; highly dense. There is a doubling of pressure amplitude at the boundary. However, energy is still conserved because no wave propagates in medium 2.
$$ Z_2 / Z_1 \rightarrow 0, Z_2 << Z_1 \rightarrow R = -1 , T = 0 $$ All energy reflected at boundary and reflected wave is completely out of phase with incident wave (think rigid end for a string). Medium 2 is easily compressed or rarefied. There is zero pressure amplitude at surface.
Note that energy is always conserved when travelling from one medium to another. So even though transmission coefficient > 1, it doesn't mean we gained energy. Energy density or intensity (W/m2) for a plane wave can be calculated as: $$ I = p^2 / 2Z $$